The given equation is quadratic and nature of roots of quadratic equation are dependant on its discriminant. Writing the equation in standard form:

Finding the discriminant:
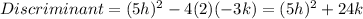
The roots of a quadratic equation are real and distinct if the value of its discriminant is greater than 0.
If we observe the value of discriminant, it is a sum of two terms in this case. The first term is square of (5h), which will always be a positive term or zero if h is zero. The second term is 24k. The value of 24k will always be positive for positive values of k.
Thus for positive values of k, the discriminant of given equation is always positive and thus we can say the root of given equation will always be real and distinct for positive values of k.