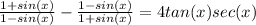Question

Prove that 1+sinx/1-sinx -1-sinx/1+sinx=4tanxsecx

Answer 1

If interpreted as shown, the order is shown in the lines following
1+sin(x)/1-sin(x)-1-sin(x)/1+sin(x)
=1 + ((sin(x))/1) - sin(x) -1 - (sin(x)/1) + sin(x)
which is completely meaningless for the purpose of this question.

The left-hand side is

`(<span>1+sin(x))/(1-sin(x))-(1-sin(x))/(1+sin(x))`
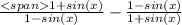
common denominator is (1-sin(x))(1+sin(x)), so

`=((1+sin(x))(1+sin(x)-(1-sin(x))(1-sin(x)))/((1+sin(x)(1-sin(x))`

`=((1+sin(x))^2-(1-sin(x))^2)/((1+sin(x)(1-sin(x))`

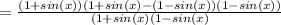
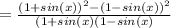
`=((1+1)(2sin(x)))/((1-sin^2(x))` using a^2-b^2=(a+b)(a-b)

`=(4sin(x))/(cos^2(x))`

`=(4tan(x))/(cos(x))`

`=4tan(x)sec(x)`

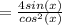
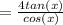
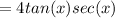
Therefore

`(1+sin(x))/(1-sin(x))-(1-sin(x))/(1+sin(x))=4tan(x)sec(x)`