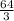First find intersection by equating values of y^2,
x+1=7-x
Solve for x
x=3
consequently
y^2=7-x=4 =>
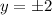
The intersection points of the two curves are therefore (3,2) and (3,-2).
The area enclosed by the two curves is therefore obtained by integration within appropriate limits.
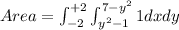
![=\int_(-2)^(+2) [x]_(y^2-1)^(7-y^2)dy](https://img.qammunity.org/2019/formulas/mathematics/college/mklxnuzeot2puwni12b9m8e7uzeite9y10.png)
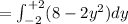
![=[8y-(2y^3)/(3)]_(-2)^(2)](https://img.qammunity.org/2019/formulas/mathematics/college/7xjt3jz99qqxrwd3x3edgyjf0uao66li7f.png)
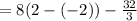
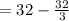
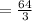
Answer: Area of between the two curves is