Question

Ezra scores 680 on the mathematics portion of the sat. the distribution of sat math scores in recent years has been normal with a mean of 518 and a standard deviation of 114. what is the z-score for ezra's sat math score?

Answer 1

The z-score is given by:


`z = (x-\mu)/(\sigma)`

where z is the z-score, x is the value whose z-score we want to calculate, μ is the mean, and σ is the standard deviation.

Hence, in your example:


`z = (680-518)/(114) =1.42`

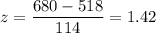
The z-score of a value is the number of standard-deviations the value is above the mean. In this case, Ezra's score is 1.42 standard-deviations above the mean.

This standardized value allows you to answer questions like: "Is Ezra's score a high score?" Well, it's obviously above the mean (162 points above the mean). But, is that a high difference? With the z-score you know that it is 1.42 standard-deviations above the mean. In a normal distribution, only 16% of the values are 1 standard deviation or more above the mean, and only 2.3% are above 2 standard deviations or more above the mean. Hence, Ezra's is a high score (between the 16% and the 2.3% best scores).