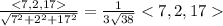Question

Find a unit vector that is orthogonal to both u and v. u = −8, −6, 4 v = 10, −18, −2

Answer 1

A vector w orthogonal to u and v can be obtained by the cross product of u and v, namely u x v. Subsequently, u x v may be reduced to a unit vector.

u<-8,-6,4>
v<10,-18,-2>

w=u x v
=
i j k
-8 -6 4
10 -18 -2
=<12+72, 40-16, 144+60>
=<84, 24, 204>
=12 < 7,2,17>

Check that w is orthogonal to u and v
w.u = 12<7,2,17><-8,-6,4> = 12(-56-12,68)=0
w.v = 12<7,2,17><10,-18,-2> = 12(70-36-34)=0
Therefore w is orthogonal to both u and v.

Unit vector of w

`(<7,2,17>)/(√(7^2+2^2+17^2))=(1)/(3√(38))<7,2,17>`