Question

Mathematics, the distance between one point (a) and another point (b), each with coordinates (x,y), can be computed by taking the differences of their x coordinates and their y coordinates and then squaring those differences. the squares are added and the square root of the resulting sum is taken and... voila! the distance. assume that point has already been defined as a structured type with two double fields, x and y. define a function dist that takes two point arguments and returns the distance between the points they re

Answer 1

(X1 , Y1)
(X2, Y2)

Distance =
`√((X1-X2)^) + (Y1-Y2)^(2) }`

Answer 2

`d=\sqrt{(y_(2) -y_(1) )^(2)+(x_(2) -x_(1) )^(2)  }`

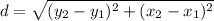
Explanation:

A relation that returns a distance between two points given is:

`d=\sqrt{(y_(2) -y_(1) )^(2)+(x_(2) -x_(1) )^(2)  }`.

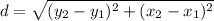Where the points are generally:
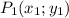`P_(1) (x_(1);y_(1))` and
`P_(2) =(x_(2),y_(2))`

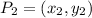
This given relation is from a Pythagoras Theorem applied to a right rectangle (image attached), where c is the distance between the two points, that's why it has a squared root and the sum of two squared difference of each coordinate.

The second image shows how the relation is develop.