Answer: The statement "The graph of function is negative on
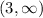 " is correct.
" is correct.
Step-by-step explanation:
The polynomial is defined as
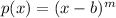 , where b is the root of the polynomial with multiplicity m.
, where b is the root of the polynomial with multiplicity m.
It is given polynomial function has a root of –5 with multiplicity 3, a root of 1 with multiplicity 2, and a root of 3 with multiplicity 7. The leading coefficient is negative.
From the given information the polynomial is defined as,
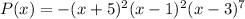
The above polynomial has 3 roots that divides the number line in 4 intervals.
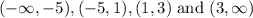
Since the leading coefficient is negative, therefore the end behaviour of the polynomial is defined as,
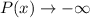 as
as
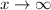
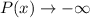 as
as
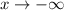
It means in the first and last interval the function must be negative.
The graph of the polynomial shown the figure.
From figure it is noticed that the graph of the function is negative on
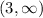 .
.