Answer:
Option D : Equation B and Equation D.
Explanation:
We are given that four equations A,B,C and D
The equation of a line which passing through the two points
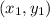 and
and
 is given by
is given by

Using this formula we obtain the equation of line A ,B,C and D
The line A which passing through the points (-6,16) and (9,-4) is given by
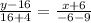
Where
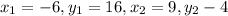
The equation of line A is given by
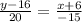
The equation of line A is given by
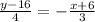
Denominator on both side divided by 5
The equation of line A is given by
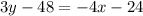
The equation of line A is given by
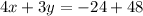
The equation of line A is given by
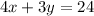
The equation of line B which passing through the points (-2,20) and (8,0) is given by
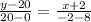
Where

The equation of line B is given by

The equation of line B is given by
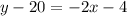
The equation of line B is given by
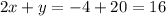
The equation of a line B which passing through the points (-2,20) and (8,0) is given by

The equation of line C which passing through the points (-7,-6) and (6,20) is given by
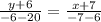
where
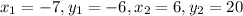
The equation of a line C is given by
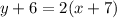
The equation of a line C is given by
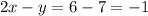
The equation of line C which passing through the points (-7,-6) and (6,20) is given by

The equation of a line D which passing through the points (7,20) and (0,-7) is given by

Where
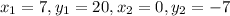
The equation of a line D is given by
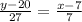
The equation of line D is given by

Using cross multiply method
The equation of a line D is given by
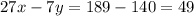
The equation of a line D which passing through the points (7,20) and (0.-7) is given by
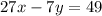
From graph we can see line B and D are intersect at point (4,8).Therefore, the solution of equation B and equation D is (4,8).
Hence, option D is correct.