Question

The measures of the sides of a triangle are in the extended ratio 2 : 5 : 11, The perimeter is 90ft. Which of the following lengths is the shortest side?

A. 2 feet

B. 10 feet

C. 5 feet

Answer 1

Add the proportion
2+5+11=18
Divide 90 by 18
Multiply the result of 90/18 by the shortest side (2 in this case) to get the final answer.

Answer 2

Shortest side of the triangle is 10 feet .

Option (B) is correct .

Explanation:

As given

The measures of the sides of a triangle are in the extended ratio 2 : 5 : 11 .

The perimeter is 90ft.

Let us assume that the x be the multiple of all sides .

Than,

One side of the triangle = 2x

Second side of the triangle = 5x

Third side of the triangle = 11x

As the perimeter of a triangle is the sum of all three sides of a triangle .

Thus

2x + 5x + 11x = 90

18x = 90

`x = (90)/(18)`

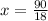
x = 5

One side of the triangle = 2x

= 2 × 5

= 10 feet

Second side of the triangle = 5x

= 5 × 5

= 25 feet

Third side of the triangle = 11x

= 11 × 5

= 55 feet

Therefore shortest side of the triangle is 10 feet .

Option (B) is correct .