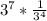Answer:
The expression equivalent to
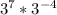 is
is
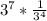
Explanation:
To answer this question, we notice that we have two factors multiplying each other. On one hand we have 3⁷, and on the other hand we have 3⁻⁴.
As the two factors are powers of the number 3, we have the following identities:

and
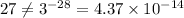
which discard that expression. We also know that if we multiply two factors with the same sign, we would get a positive number, so this discards the expression 3⁷x (-3⁴), as this resulting number will be negative (and 9 is positive).
Finally, we can write the following identity
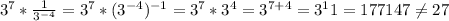
Therefore the correct answer is