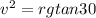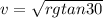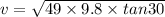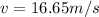Question

You are riding in a school bus. as the bus rounds a flat curve at constant speed, a lunch box with a mass of 0.470 kg suspended from the ceiling of the bus by a string of length 1.75 m is found to hang at rest relative to the bus when the string makes an angle of 30.0 ∘ with the vertical. in this position the lunch box is a distance 49.0 m from the center of curvature of the curve.

Answer 1

Missing question: " What is the speed v of the bus?"

Solution:
Let's solve the problem by writing the equilibrium conditions on both x- and y- axis:

`mg=T cos \alpha`

`m (v^2)/(r)=T sin \alpha`
where
`mg` is the weight of the lunch box,
`m (v^2)/(r)` is the centripetal force, T is the tension of the string and
`\alpha=30^(\circ)`.

The radius r is the one with respect to the vertical position of the string, therefore

`r=L sin30^(\circ)=0.875 m`.

From the first equation we find

`T= (mg)/(cos \alpha)`
and if we replace this into the second one, we find

`m (v^2)/(r)=mg \tan \alpha`
from which we can find the velocity:

`v= √(rg \tan \aplha)= \sqrt{(0.875m)(9.81m/s^2)(\tan 35^(\circ))}=2.45 m/s`

Answer 2

Here as we know that

m = mass of the box = 0.470 kg

L = Length of the string = 1.75 m

r = radius of the path = 49 m

`\theta` = angle of the thread

Now from the condition of equilibrium of lunch box with respect to bus we can say

`Tsin30 = (mv^2)/(r)`

`Tcos30 = mg`

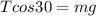
now divide the above two equations

`tan30 = (v^2)/(rg)`

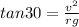
solving the above equation for velocity

`v^2 = rg tan30`

`v = √(rgtan30)`

`v = √(49* 9.8* tan30)`

`v = 16.65 m/s`