Question

Please help me with this problem asap

Answer 1

"When 3 is substracted" can be written as minus 3
"One third of a number" can be written as
`(1)/(3) n`
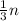
"The result is less than 6" can be written as < 6

Therefore we put them up together, the inequality will be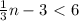

`(1)/(3)n-3\ \textless \ 6`

Solve for the value of n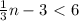

`(1)/(3)n-3\ \textless \ 6`
add both side with 3

`(1)/(3)n-3+3\ \textless \ 6+3`

`(1)/(3)n\ \textless \ 9`
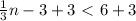
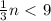
multiply both side by 3

`$3*\ (1)/(3)n\ \ \textless \ 3 *\ 9$`
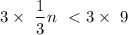
n < 27

The correct answer is first option

`\boxed{\boxed{ (1)/(3)n-3\ \textless \ 6;n\ \textless \ 27 }}`

Answer 2

The correct answer is the 3rd one