Question

The driver of a 1,000 kg car travelling at a speed of 16.7 m/s applies the car's brakes when he sees a red light. the car's brakes provide a frictional force of 8,000 n. determine the stopping distance of the car.

Answer 1

Energy conservation :
kinetic energy Ek = braking work W
mV^2 = 2Fb*x
x = mV^2/2Fb = 1000*16.7^2/16.000 = 17.43 meters

Answer 2

1.04 meters

Step-by-step explanation:

Thinking process:

Gathering the data

mass = 1 000 kg

speed, u = 16.7 m/s

Frictional force = 8 000 N

distance, s = ?

final velocity = 0 (car stops)

We know that the final velocity is calculated as:
`v^(2) = u^(2) + 2as`

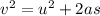
But, a = negative (declaration)

And F = ma

`8 000 = 1000 (a)\\ a = -8 m^(-2)`

substituting, 0 = (16.7) - 2 (8) (s)

-16.7 = -16s

s = 1.04 m

Stopping distance = 1.04 meters