Question

Use the formula to evaluate the infinite series. Round your answer to the nearest hundredth if necessary. 72 + 12 + 2 + . . .

Answer 1

To find the sum of an infinite series, use this following formula
S∞ =
`(a_(1))/(1-r)`
with S∞ as the sum of infinite series, a₁ as the first term of the series, and r as the ratio.

First, find the ratio of the series
The ratio can be defined using division of the nth term by the (n-1)th term. Or if you use a₂, the divisor will be a₍₂₋₁₎ = a₁
r = a₂/a₁
r =
`(12)/(72)`
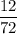
r =
`(1)/(6)`
The ratio of the series is 1/6

Second, calculate the sum using the formula above.
S∞ =
`(a)/(1-r)`

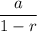
Plug in the numbers
S∞ =
`(72)/(1- (1)/(6) )`

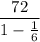
Write the division horizontally
S∞ = 72 ÷
`(1-(1)/(6))`

1 can be written as 6/6
S∞ = 72 ÷
`((6)/(6) -(1)/(6) )`
S∞ = 72 ÷
`(5)/(6)`

Change the division into multiplication
S∞ = 72 ×
`(6)/(5)`
S∞ =
`(432)/(5)`
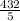
S∞ = 86.4
The sum of the series is 86.4