Question

A wooden dowel (cylinder) has a diameter of 2.20 cm. it floats in water with 0.60 cm of its diameter above water. determine the density of the dowel.

Answer 1

To determine the density of the dowel, we can use the principle of buoyancy. Given that 0.6 cm of the dowel's diameter is above water, we can calculate the volume of the dowel and then determine its density.

Step-by-step explanation:

To determine the density of the wooden dowel, we can use the principle of buoyancy. When an object floats in a fluid, the weight of the fluid displaced by the object is equal to the weight of the object itself. We can use this principle to find the volume of the dowel and then calculate its density.

Given that 0.6 cm of the dowel's diameter is above water, we can determine that the height of the dowel submerged in water is 2.2 cm - 0.6 cm = 1.6 cm.

The volume of the dowel can be calculated using the formula for the volume of a cylinder: V = πr^2h, where r is the radius (half the diameter) and h is the height.

In this case, the radius is 2.20 cm / 2 = 1.10 cm.

Substituting the values into the formula, we get V = π(1.10 cm)^2(1.6 cm) = 6.09 cm^3.

Now, we can calculate the density using the formula: density = mass/volume. Since the density of water is 1 g/cm^3, the mass of the dowel can be found by multiplying the volume by the density of water: mass = 6.09 cm^3 * 1 g/cm^3 = 6.09 g.

Finally, we can find the density of the dowel by dividing the mass by the volume: density = 6.09 g / 6.09 cm^3 = 1 g/cm^3.

Answer 2

In the image the situation is illustrated, also provided is a simple proof for the circle segment area. The problem can be solved without actually knowing the lenght of the dowel.
We will only care for the circular seection of the dowel which is partially submerged. Recall that for a floating body the weight of displaced water is equal to the body's weight.
For the dowel's weight we have:

`D_w=m.g`
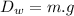
where g is the gravitational constant and m the dowel's mass.

Now for the displaced water weight:

`W_w=V_(displaced).\rho_(water).g`
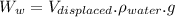
where
`\rho_(water)` is the water density, which happens to be
`1000kg/m^3`.
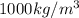
we now have the following:

`V_(displaced).\rho_(water).g=m.g`

`\implies V_(displaced).\rho_(water)=m`
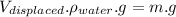
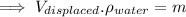
but:

`m=\rho_(dowel).V`
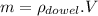
being V the volume of the dowel, putting the above toghether gives us:

`V_(displaced).\rho_(water)=V.\rho_(dowel)`
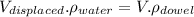
Now
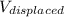
`V_(displaced)` is the volume of the dowel that is submerged.The fraction of the dowel submerged will be according to the image:

`(\pi r^2-(1)/(2)r^2(\theta-sin\theta))/(\pi r^2)=((\pi-(1)/(2)\theta+sin\theta))/(\pi)`
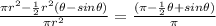
So the dowel's volume that is submerged is:

`V_(displaced)=V_(submerged)=((\pi-(1)/(2)\theta+sin\theta))/(\pi).V`

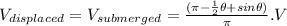
Plug this into the previous expression to get:

`((\pi-(1)/(2)\theta+sin\theta))/(\pi).V.\rho_(water)=V.\rho_(dowel)\\ \implies \rho_(dowel)=((\pi-(1)/(2)\theta+sin\theta))/(\pi).\rho_(water)`

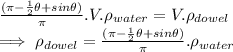
There's only one thing missing, the
`\theta` angle. Refer to the second image to get the following expression:

`\theta=2Acos((1)/(2r))`
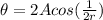
where r is the dowel's radius.
Plugging the above in the expression for the dowel's density we get:

`(\left(\pi-Acos((1)/(2r))+sin\left[ Acos\left( (1)/(2r)\right )\right]\right))/(\pi).\rho_(water)\\`
where:


`sin\left[ Acos\left( (1)/(2r)\right)\right]=\sqrt{1-\left( (1)/(2r)\right)^2}`
We finally get:

`\rho_(dowel)=\frac{\left(\pi-Acos((1)/(2r))+\sqrt{1-\left( (1)/(2r)\right)^2}\right)}{\pi}.\rho_(water)`
This result is in
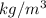
`kg/m^3`.