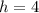Question

What are the solutions to the equation? 2h2+8h=64 Enter your answers in the boxes. h = and

Answer 1

2h²+8h=64
h²+4h=32
h²+4h-32=0
factor: (x+8)(x-4)=0
x=-8 or x=4

Answer 2

The solutions to the equation are:
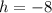`h= -8` and
`h=4`

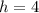
Step-by-step explanation

`2h^2 +8h= 64`

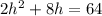
First we will divide all terms in both sides by 2. So,

`(2h^2)/(2) + (8h)/(2)= (64)/(2) \\ \\ h^2 + 4h = 32`

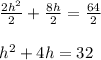
Then we will subtract 32 from both sides and then factor out the whole left side. So,

`h^2 +4h -32 = 32- 32\\ \\ h^2 +4h -32 =0 \\ \\ h^2 +8h -4h -32 =0 \\ \\ h(h+8)-4(h+8)=0 \\ \\ (h+8)(h-4)= 0`

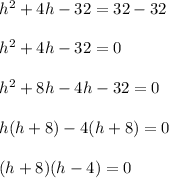
Now we will apply the Zero product property. So,

`h+8 =0 \\ \\h= -8 \\ \\ or, h-4=0\\ \\ h= 4`

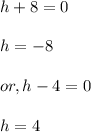
So, the solutions are:
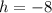`h= -8` and
`h=4`