Question

Lisa will rent a car for the weekend. She can choose one of two plans. The first plan has an initial fee of $ 59.98 and costs an additional $ 0.08 per mile driven. The second plan has an initial fee of $ 49.98 and costs an additional $ 0.12 per mile driven. How many miles would Lisa need to drive for the two plans to cost the same?

Answer 1

We can solve by making an equation.


`0.08x + 59.98 = 0.12x + 49.98`

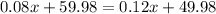
Move terms and change its sign when crossing the equal sign (math rules).


`0.08x + 59.98 = 0.12x \\ \: \: \: \: \: \: \: \: \: \: \: \: - \: 49.98 = 10`

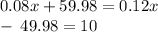
Move over the over number,


`10 = 0.12x \\ \: \: \: \: \: \: - \: 0.08x = 0.04x`

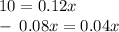
Let's rewrite the equation,


`10 = 0.04x`

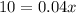
Divide both sides by 0.04 to isolate the variable,


`250 = x`

~~

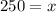
Answer :

Lisa would need to drive 250 miles for the two plans to cost the same.

~~

I hope that helps you out!!

Any more questions, please feel free to ask me and I will gladly help you out!!

~Zoey