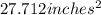Question

What is the area, rounded to the nearest tenth of square inch, of an equilateral triangle that has a perimeter of 24 inches?

Answer 1

`27.712 inches^2`

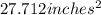
Explanation:

Perimeter of equilateral triangle =
`3 * side`

We are given that an equilateral triangle that has a perimeter of 24 inches

So,
`3 * side=24`

`Side=(24)/(3)`

`Side=8`

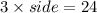
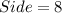
Area of equilateral triangle =
`(√(3))/(4)a^2`

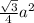
a is the side

So, Area of equilateral triangle =
`(√(3))/(4)(8)^2`

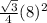
So, Area of equilateral triangle =
`27.712 inches^2`

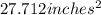
Hence the area of equilateral triangle is
`27.712 inches^2`

Answer 2

Answer: 27.7 square inches.

Explanation:

Let 'a' be the side of equilateral triangle.

Then the perimeter of the triangle = a+a+a=3a

Given: Perimeter of the equilateral triangle = 24 inches

`\\\Rightarrow3a=24\\\\\Rightarrow\ a=8\ inches`

We know that the area of a equilateral triangle is given by :-

`A=(√(3) a^2)/(4)\\\\\Rightarrow\ A=(√(3) (8)^2)/(4)\\\\\Rightarrow\ A=27.71281292\approx27.7\ in.^2`