For any polynomial
 ,
,
 is a root of the polynomial only if
is a root of the polynomial only if
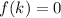 .
.
To determine which of the given values is a root of the polynomial ,
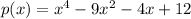 ,
,
we just have to evaluate the
 for each of these values and see if the output is zero.
for each of these values and see if the output is zero.
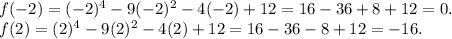
Since
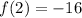 , we know that
, we know that
 is not a root of this polynomial.
is not a root of this polynomial.
Since
 , we know that
, we know that
 is a root of this polynomial.
is a root of this polynomial.