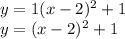Question

What is the equation of the following graph in vertex form? parabolic function going down from the left through the point zero comma five and turning at the point two comma one and continuing up towards infinity

Answer 1

By your description i would say y = ( x - 2)^2 + 1

Answer 2

`y=(x-2)^(2)+1`

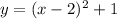
Explanation:

The general form for the parabolic function on its vertex form is:

`y=a(x-h)^2+k`

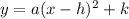
where:

`(h,k)=vertex\\`

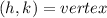
the vertex will be where the parabolic function stops going down and starts to go up towars infintiy. In the problem this vertex is given as described and it is

`(2,1)`

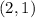
we have left to find the
`a`. We can find it by using the point that was given to us in the problem thet the parabole goes through
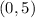`(0,5)` and replacing it in the equation for
`x` and
`y` like this:

`y=a(x-h)^2+k\\5=a(0-2)^2+1\\5=a(-2)^2+1\\5=a(4)+1\\a(4)=5-1\\a(4)=4\\a=(4)/(4)\\ a=1`

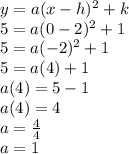
now we replace
`a` and
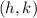`(h,k)` in the general form:

`y=1(x-2)^2+1\\y=(x-2)^2+1`