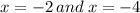Question

PLEASE HELP

The graph shows the function

f(x)=−6x−12 and g(x)=(1/2)^x−4 .

What are the solutions of the equation −6x−12=(1/2)^x−4 ?

Answer 1

`x = - 2 \\ x = - 4`

Answer 2

ANSWER

The solutions are;


`x = - 2 \: and \: x = - 4`

Step-by-step explanation


The two functions are, the linear function,


`f(x) = - 6x - 12`

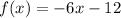
and the exponential function,



`g(x) = {( (1)/(2) )}^(x) - 12`



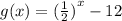
We want to use the graph of these two functions to find the solution of the equation,





`- 6x - 12 = {( (1)/(2) )}^(x) - 12`

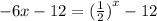
The solution is the x-values of the intersections of the two graphs.

The points of intersections are


`(-2,0) \: \: and \: \: (-4,12)`

The x-values of these points are;




`x = - 2 \: and \: x = - 4`