Question

Given that EFGH is a kite, what is m∠EHG?

A) 68°
B) 88°
C) 102°
D) 198°

Answer 1

For a better understanding of the solution given here please find the attached file which has the diagram of the kite EFGH.

As can be seen from the diagram,
`\angle FEH=\angle FGH=102^(\circ)`

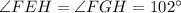
Also, it is given that
`\angle EHG=68^(\circ)`

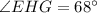
We are required to find the
`\angle EFG`.

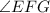To proceed we know that a kite is a quadrilateral and in a quadrilateral the sum of the interior angles is 360 degrees. Thus, we will get:

`m\angle FEH+m\angle EHG+m\angle FGH+m\angle EFG=360^(\circ)`

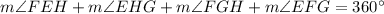
Plugging in the given values we get:

`102^(\circ)+68^(\circ)+102^(\circ)+m\angle EFG=360^(\circ)`

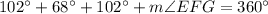
This will give:

`m\angle EFG=88^(\circ)`

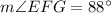
Therefore, Option B is the correct option.

Answer 2

Assuming angle F is 68°, angle H will be
.. 360° -2*102° -68° = 88° . . . . . . . . selection B