Question

Subtract (3u-3)(u+3)

Answer 1

__________________________________________________________
Note 1: A constant number (A number without an exponent) will have the degree of 0. Always.
Note 2: A variable without a visible exponent obtains an exponent of 1. Ex. x =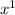
`x^(1)`
Note 3: The operation sign before a coefficient/constant indicates if it's positive or negative. If no subtraction (or even addition) sign is in front of a value, it's positive. If a subtraction sign stands in front of a value, the value is negative. If an addition sign stands in front of the value, the value is negative.
Note 4: When a number is not standing in front of a variable, it translates to 1 times that variable. Ex. x = 1x
Note 5: coefficients contain a number and a variable.
___________________________________________________________

1: Remove Parentheses [we do this by distributing what's in the parentheses by 1. For the first part (3u-3), you can simply just remove the parentheses because it doesn't affect what's in the parentheses whatsoever. For the second one, however, you distribute -1 to the second part (u+3) which gets us -u - 3]

Answer: 3u-3 - u - 3

2: Order, sort, and combine the like terms.
View attachment.

3: Solve.
3u - u - 3 - 3
(3u - u) -3 - 3

`3u - (1)u = 3 - 1, u = 2u`
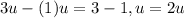Answer:
`2u`
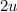
2u (-3 - 3 [= -6])
Answer: -6

So 2u - 6