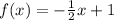Question

Write the​ slope-intercept equation of the function f whose graph satisfies the given conditions.

Answer 1

To find the slope of the perpendicular line, we must find the slope of the line with x-intercept of 2 and y-intercept of -4.

Let's use rise/run to find the slope. The run is 2, and the rise if 4 (yes, positive 4).

4/2 = 2

So, the slope of the original line is 2. The other line must have a slope that is the negative reciprocal of that, which will be -1/2.

Let's start making our equation by using point-slope form.

For a line with slope m and that passes through
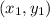
`(x_1,y_1)`, the point slope form equation is the following:


`y-y_1=m(x-x_1)`

We know the passing point and the slope. Now, let's plug them into the point-slope form formula.


`y-4=- (1)/(2) (x+6)`

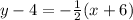
Distribute.


`y-4= -(1)/(2) x-3`

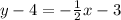
Now, add both sides by 4.


`y= -(1)/(2) x+1`

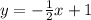
Replace y with f(x)


`f(x)=- (1)/(2)x+1`