Question

Charge of a uniform density (8.0 nc/m2) is distributed over the entire xy plane. a charge of uniform density (3.0 nc/m2) is distributed over the parallel plane defined by z = 2.0 m. determine the magnitude of the electric field for any point with z = 3.0 m.

Answer 1

The electric field generated by an infinite plane uniformly charged is

`E= (\sigma)/(2\epsilon _0)`
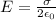
where
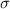
`\sigma` is the charge density of the plane, while
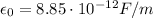
`\epsilon _0 = 8.85\cdot 10^(-12) F/m` is the vacuum permittivity.

Let's calculate the electric field of the first (xy) plane:

`E_1 = (\sigma_1)/(2 \epsilon _0)= (8\cdot 10^(-9) C/m^2)/(2 \cdot 8.85\cdot 10^(-12) F/m)= 452.0 V/m`

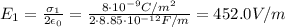
And now the electric field due to the second (z=2.0 m) plane:

`E_2 =(\sigma_2)/(2 \epsilon _0)= (3\cdot 10^(-9) C/m^2)/(2 \cdot 8.85\cdot 10^(-12) F/m)= 169.5 V/m`

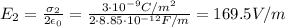
The electric field of the two planes does not depend on the distance. Also, the charges on the two planes have same sign, so at z=3.0 m (and at every point with z>2.0m) the two fields point into the same direction and the total electric field is simply the sum of the two fields:

`E_(tot) = E_1 + E_2 =621.5 V/m`