Question

Which expression defines the arithmetic series 1 + 5 + 9 + . . . for seven terms?

Answer 1

The first 7 terms will be 1+5+9+13+17+21+25

`\sum\limits^6_(i=0)4i+1 = \sum\limits^7_(i=1)4i-3`
Hope this is what you're looking for

Answer 2

`a_n=1+(n-1)4`

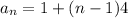
Explanation:

Given : arithmetic series 1 + 5 + 9 + . . .

To Find: Which expression defines the arithmetic series 1 + 5 + 9 + . . . for seven terms?

Solution :

1 + 5 + 9 + . . .

a = first term = 1

d = common difference = 5-1=9-5=4

Formula of nth term =
`a_n=a+(n-1)d`

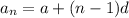
So, formula for nth term for given sequence
`a_n=1+(n-1)4`

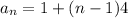
So,
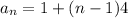`a_n=1+(n-1)4` defines the arithmetic series 1 + 5 + 9 + . . . for seven terms

Now, formula of sum of n terms in A.P. =
`(n)/(2)(2a+(n-1)d)`

So, the sum of seven terms in given series =
`(7)/(2)(2*1+(7-1)4)`

=
`(7)/(2)*(26)`

=
`7*13`

=
`91`

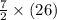
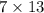
Thus the expression for the sum of seven terms =
`(n)/(2)(2a+(n-1)d)`