Answer:
A, the rectangular room will be in the shape of cuboid, whose dimension are
Length = 20 ft, Width=48 ft and Height = 10 ft
Length of Diagonal of floor
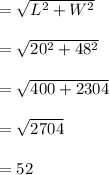
Length of Diagonal of floor=52 ft
Length of diagonal of Room

Length of diagonal of Room=52.95 ft