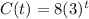Question

In a laboratory, under favorable conditions, a bacteria grows at an exponential rate. the number of cells C in the population is modeled by the function C(t)=ab^t, where a and b are constants and t is measured in hours.

T                C(t)

---            -------
0                 8
-----           --------
1                 24

Which function can be used to find the number of cells of bacteria in the population at time t?


A. C(t)=8(1)^t

B. C(t)=24(1)^t

C. C(t)=8(3)^t

D. C(t)=24(3)^t

Answer 1

Eponential model is given by
`C(t)=8(3)^t`

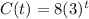
C is the correct option.

Explanation:

From the given table, we have

For t = 0, C = 8

For t = 1, C = 24

The given model is
`C(t)=ab^t`

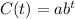
Plugging, t = 0, C = 8 in the equation, we get

`8=ab^0\\8=a\cdot1\\a=8`

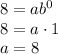
Now, plugging t = 1, C = 24 and a = 8 in the given exponential model

`24=8b^1\\24=8b\\b=3`

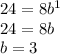
Therefore, the exponential model is given by

`C(t)=8(3)^t`

Answer 2

Selection C is appropriate.

_____
A. The population is constant at 8.

B. The population is constant at 24.

C. Matches the problem description.

D. The initial population is 24 and after 1 hour is 72.