Question

the dimensions of a rectangle can be expressed as x+6 and x-2. if the area of the rectangle is 65in^2, find the dimensions of the rectangle.

Answer 1

`\bf \textit{area of a rectangle}\\\\ A=length\cdot width\qquad \boxed{A=65~in^2}\qquad 65=(\stackrel{length}{x+6})(\stackrel{width}{x-2}) \\\\\\ 65=x^2+4x-12\implies 0=x^2+4x-77 \\\\\\ 0=(x+7)(x-11)\implies x= \begin{cases} -7\\ \boxed{11} \end{cases}`

it cannot be -7, because that would give a negative value for either dimension, and a dimension for the rectangle cannot be negative.

so, the dimensions would be (11) + 6 and (11) - 2.

Answer 2

The dimensions of the rectangle is 13 length and 5 breadth.

Explanation:

Given : The dimensions of a rectangle can be expressed as x+6 and x-2. If the area of the rectangle is 65 in².

To find : The dimensions of the rectangle ?

Solution :

Let length l= x+6

Breadth b= x-2

The area of the rectangle is A= 65 in².

The area of the rectangle is given by,

`A=l* b`

`65=(x+6)* (x-2)`

`65=x^2-2x+6x-12`

`x^2+4x-12-65=0`

`x^2+4x-77=0`

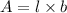
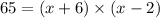
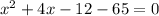
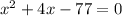
Applying middle term split,

`x^2+11x-7x-77=0`

`x(x+11)-7(x+11)=0`

`(x+11)(x-7)=0`

`x=-11,7`

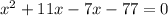
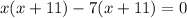
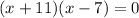
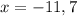
The value of x=7 as we reject -11.

Length l= x+6=7+6=13 inches

Breadth b= x-2=7-2=5 inches

The dimensions of the rectangle is 13 length and 5 breadth.