Question

Find x and y, given that line WS and line VT are parallel. Show all work!

Answer 1

In the given diagram, the traingles USW and UTV are similar triangles and thus the following ratio equality applies to them.

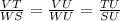`(VT)/(WS) =(VU)/(WU)=(TU)/(SU)`..........(Equation 1)

Checking the diagram given, we see that:

VT=y, WS=22, VU=8, ST=x-2

WU=WV+VU=12+8=20

TU=5

SU=ST+TU=(x-2)+5=x+3

Thus, substituting the required values in (Equation 1) we get:

`(y)/(22)=(8)/(20)=(5)/(x+3)`

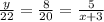
Now, as can be clearly seen, to find y we will use the first two ratios as:

`(y)/(22)=(8)/(20)`

`y=(8* 22)/(20)=8.8`

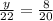
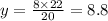
In a similar manner, to find the value of x we can use the last two ratios:

`(8)/(20)=(5)/(x+3)`

After cross multiplication we get:

`5* 20=8(x+3)`

Which can be simplified as:

`x+3=(100)/(8) =12.5`

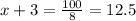
Thus,
`x=12.5-3=9.5`

Therefore, the required answer is:

x=9.5 and y=8.8