Question

A ball is rolled at a speed of 12 m/seconds after 36 seconds it comes to stop what is the acceleration of the ball

Answer 1

Approximately
`(-0.33)\; {\rm m\cdot s^(-2)}` (
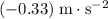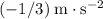`(-1/3)\; {\rm m\cdot s^(-2)}`) on average.

Step-by-step explanation:

Acceleration is the rate of change in velocity.

For the ball in this question:

• Initial velocity:
  `u = 12\; {\rm m\cdot s^(-1)}`.
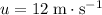• Final velocity:
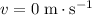  `v = 0\; {\rm m\cdot s^(-1)}` since the ball has stopped.
• Time required:
  `\Delta t = 36\; {\rm s}`.

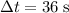Subtract the initial velocity
`u` from the final velocity
`v` to find the change in velocity:

`\begin{aligned}(\text{change in velocity}) &= (\text{final velocity}) - (\text{initial velocity}) \end{aligned}`.

`\begin{aligned}\Delta v &= v - u \\ &= 0\; {\rm m\cdot s^(-1)} - 12\; {\rm m\cdot s^(-1)} \\ &= (-12)\; {\rm m\cdot s^(-1)} \end{aligned}`.

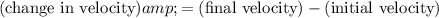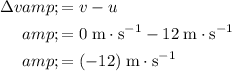(Note that the change in velocity is negative because the final velocity
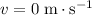`v = 0\; {\rm m \cdot s^(-1)}` is more negative than the initial velocity
`u = 12\; {\rm m\cdot s^(-1)}`.)

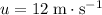To find the average acceleration
`a` (average rate of change in velocity,) divide the change in velocity
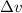`\Delta v` by the time
`\Delta t` required to achieve such change:

`\begin{aligned}(\text{average acceleration}) &= \frac{(\text{velocity change})}{(\text{time required for change})}\end{aligned}`.

`\begin{aligned} a &= (\Delta v)/(\Delta t) \\ &= \frac{(-12)\; {\rm m\cdot s^(-1)}}{36\; {\rm m\cdot s^(-1)}} \\ &\approx (-0.33) \; {\rm m\cdot s^(-2)}\end{aligned}`.

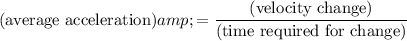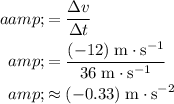(Average acceleration is negative since velocity is becoming less positive.)