Question

Convert the polar representation of this complex number into its standard form.

2(cos(7pi/6)+isin(7pi/6))

A.) -sqrt(3)-i
B.) 1-sqrt(3) i
C.) -sqrt(3)/2-1/2i
D.) sqrt(3)-1
*Need help please*

Answer 1

`2(cos((7 \pi)/(6))+i\ sin((7 \pi)/(6)))\\\\2((-(√(3))/(2))+i(-(1)/(2)))\\\\\\-√(3)-i`

Answer 2

Option A is correct

The standard form is

`2(\cos{(7\pi)/(6)}+i\sin{(7\pi)/(6)})=-\sqrt3-i`

Explanation:

Given the polar representation of complex number

`2(\cos{(7\pi)/(6)}+i\sin{(7\pi)/(6)})`

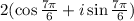
we have to convert the above polar representation in standard form.

The standard form of a complex number is a+ib

where a is the real part and bi is the imaginary part.

`2(\cos{(7\pi)/(6)}+i\sin{(7\pi)/(6)})`

`=2\cos{(7\pi)/(6)}+2i\sin{(7\pi)/(6)}`

`=2* ((-\sqrt3)/(2))+2i* ((-1)/(2)}`

`=-\sqrt3-i`

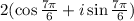
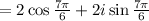
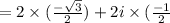
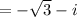
which is required standard form.

Hence, option A is correct.