Question

What is the smallest radius of an unbanked (flat) track around which a bicyclist can travel if her speed is 22 km/h and the coefficient of static friction between tires and track is 0.37?

Answer 1

First, let's put 22 km/h in m/s:


`22 (km)/(h) * (1000m)/(1km) * (1h)/(3600s)=6.11 (m)/(s)`

Now the radial force required to keep an object of mass m, moving in circular motion around a radius R, is given by


`F_(rad)=m (v^2)/(R)`

The force of friction is given by the normal force (here, just the weight, mg) times the static coefficient of friction:


`F_(fric)= mg \mu_(s)`

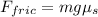
Notice we don't use the kinetic coefficient even though the bike is moving. This is because when the tires meet the road they are momentarily stationary with the road surface. Otherwise the bike is skidding.

Now set these equal, since friction is the only thing providing the ability to accelerate (turn) without skidding off the road in a line tangent to the curve:


`m(v^2)/(R) = mg \mu_(s) \\ \\ (v^2)/(R) = g \mu_(s) \\ \\R= (v^2)/(g \mu_(s)) \\ \\ R= (6.11)/(9.8 * 0.37)=1.685m`