Answer: 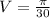 Step-by-step explanation:
Step-by-step explanation:First, we compute the points of intersection of the curves
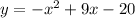
and

. Since the equation have y as their left sides,

So, the curves intersect at x = 5 and x = 4. Using the ring method
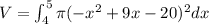
(1)
In the ring method, if the region is rotated about x-axis, we use dx in the integration and the independent variable is x. Because the independent variable is x, we use the x-coordinates of points of intersection as the limits of integration.
Note that in equation (1), we use 4 and 5 as limits of integration because the given curves
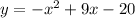
and y =0 intersect at x = 4 and x = 5.
Hence, using equation (1), the volume of the solid is given by:
![V = \int_(4)^(5){\pi(-x^2 + 9x - 20)^2}dx \\ \indent = \pi\int_(4)^(5){(x^4 -18x^3 + 121x^2 − 360x + 400)}dx \\ \indent = \pi\left [ (x^5)/(5) - (9x^4)/(2) + (121x^3)/(3) - 180x^2 + 400x + C \right ]_(4)^(5) \\ \indent \boxed{V = (\pi)/(30)}](https://img.qammunity.org/2019/formulas/mathematics/college/ftfqevo36fvd5m2xj9frdghrphgsgmpwk1.png)