PART AGeneral formula of quadratic equation
ax² + bx + c = 0
To find the discriminant of the quadratic equation shown above, use this following formula.
d =

There is a quadratic equation below
x² - 16x + 4 = 0
therefore
a = 1
b = -16
c = 4
Plug in the numbers to the formula
d =

d =
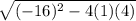
d =
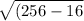
d =
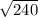
Simplify
d =
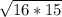
d =
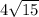 The value of the discriminant is 4√15PART B
The value of the discriminant is 4√15PART B
If the discriminant is less than zero (negative), the quadratic equation has imaginary solution.
If the discriminant is equal to zero, the quadratic equation has only one solution.
If the discriminant is more than zero (positive), the quadratic equation has two real solutions.
Because the discriminant of the quadratic equation is 4√15 and it's positive,
the quadratic equation has two real solutions.