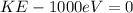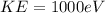Question

A proton has been accelerated from rest through a potential difference of -1000 v . part a what is the proton's kinetic energy, in electron volts?

Answer 1

kinetic energy of the proton will be 1000eV

Step-by-step explanation:

As we know that change in potential energy of a point charge when it is passed through a given potential difference is given by the formula

`\Delta U = q(\Delta V)`

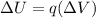
here we know that

charge is due to a proton

`q = +e`

potential difference is given by

`\Delta V = -1000Volts`

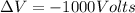
so here we will have

`\Delta U = (+e)(-1000V) = -1000 eV`

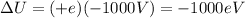
now by mechanical energy conservation law we know that

`\Delta KE + \Delta U = 0`

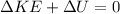
so here we have

`KE - 1000eV = 0`

`KE = 1000 eV`

Answer 2

We can apply the law of conservation of energy here. The total energy of the proton must remain constant, so the sum of the variation of electric potential energy and of kinetic energy of the proton must be zero:

`\Delta U + \Delta K=0`
which means

`\Delta K = - \Delta U`
The variation of electric potential energy is equal to the product between the charge of the proton (q=1eV) and the potential difference (
`\Delta V=-1000 V`):

`\Delta U = q \Delta V=(1 eV)(-1000 V)=-1000 eV`
Therefore, the kinetic energy gained by the proton is

`\Delta K = -(-1000 eV)=1000 eV`
And since the initial kinetic energy of the proton was zero (it started from rest), then this 1000 eV corresponds to the final kinetic energy of the proton.