Question

Two angles are supplementary. The larger angle is 15 more than 10 times the smaller angle. Find the measure of each angle.

System of Equation:



Solution:

Answer 1

Let
`x` be the smaller angle, then the larger angle is
`10x + 15` (since it is
`15` more than
`10` times the smaller angle).

Since the angles are supplementary, their sum is
`180` degrees:

`\large\qquad\quad x + (10x + 15) = 180`

Simplifying the left side:

`\large\qquad\qquad 11x + 15 = 180`

Subtracting
`15` from both sides:

`\qquad\qquad\quad\large 11x = 165`

Dividing by
`11`:

`\qquad\qquad\qquad\large\fbox{x = 15}`

So the smaller angle is 15 degrees. To find the larger angle, we substitute
`x=15` into our expression for the larger angle:

`\qquad\large\begin{aligned}10x + 15& = 10(15) + 15\\& = 150 + 15\\&= \fbox{165}\end{aligned}`

So the larger angle is 165 degrees.

`\therefore` The smaller angle is 15 degrees and the larger angle is 165 degrees.

`\blue{\overline{\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad}}`

Answer 2

Hello!

1) Let's take this problem in steps:

==> lets first set up some variable for the two angle's measure

--> let's use: 'x' and 'y'

==> two angles are supplementary

--> in other words: the sum of two angles equal 180⁰

x + y = 180

==> larger angle is 15 more than 10 times the smaller angle

--> if 'x' is the larger angle and 'y' is the smaller angle

x = 10y + 15

2) Thus our system of equations are:

`x+y=180\\x=10y+15`

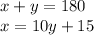
3) Let's solve our system of equations:

==> substitute x's value in terms of y from the second equation into the

first equation

`x+y=180\\\\(10y+15)+y=180\\\\10y+y+15=180\\\\11y+15=180\\\\11y=165\\\\y=15`

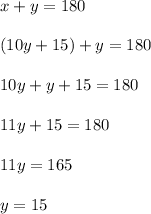
==> now substitute y's value into the first equation that we got initially

`x+15=180\\\\x=180-15\\\\x=165`

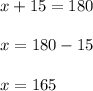
4) Therefore the two angle's measure are 165 and 15

Answer:

Two angle measure: 165⁰ and 15⁰

System of equations: look at section two

Have a great day!