For a complete understanding of the question please find the diagram in the file attached.
In the diagram a perpendicular DP is dropped from D on AB as shown.
It is given that
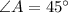 and that
and that
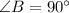 . Thus, the
. Thus, the
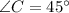 . This is because we know that the interior angles of any triangle add up to make
. This is because we know that the interior angles of any triangle add up to make
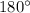 .
.
Thus,
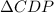 gives:
gives:
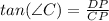
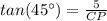
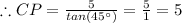
Thus, PB=CB-CP=15-5=10
Now, since,
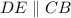 , then by corresponding angles,
, then by corresponding angles,
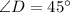
Also, we note that DE=PB=10
Thus, in
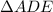 ,
,
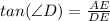
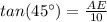
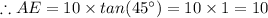
Thus, now to find the area of the triangle
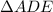 all that we have to do is use the Area formula as:
all that we have to do is use the Area formula as:
Area=
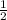 x base x height =
x base x height =
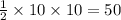 square units
square units