Question

$500 principal earning 4% compounded quarterly after 6 years

Answer 1

$634.87.

Step-by-step explanation:

We are supposed to find the total amount of an amount of $500 principal earning 4% compounded quarterly after 6 years.

To solve our given problem we will use compound interest formula to solve our given problem.

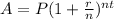`A=P(1+(r)/(n))^(nt)`, where,

A = Final amount after t years,

P = Principal amount,

r = Interest rate in decimal form,

n = Number of times interest is compounded per year,

t = Time in years.

First of all, we need to convert our given interest rate in decimal form.

`4\%=(4)/(100)=0.04`

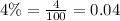
Upon substituting our given values in above formula we will get,

`A=500(1+(0.04)/(4))^(4*6)`

`A=500(1+0.01)^(24)`

`A=500(1.01)^(24)`

`A=500*1.2697346485`

`A=634.867\approx 634.87`

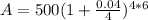
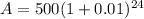
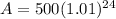
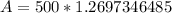
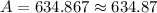
Therefore, there will be an amount of $634.87 in the account after 6 years.

Answer 2

The amount of interest earned would be $134.87 for a total of $634.87 after 6 years.

Step-by-step explanation:
The formula for compound interest is

`A=p(1+(r)/(n))^(tn)`,

where p is the principal, r is the interest rate as a decimal number, n is the number of times per year the interest is compounded, and t is the number of years.

Our principal is $500, our interest rate is 4%=4/100=0.04, n is 4, and t is 6:

`A=500(1+(0.04)/(4))^(4*6) = 500(1+0.01)^(24)=500(1.01)^(24)`

Evaluating this, we get $634.87, which means there was 634.87-500 = 134.87 earned in interest.