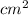Question

The pyramid shown has a square base that is 24 centimeters on each side. The slant height is 16 centimeters. What is the lateral surface area?

Answer 1

check the picture below.

the "lateral" area, or "sides" area, is just the area of all the four triangular faces, and it doesn't include the bottom or base of the pyramid.

however, notice, each triangular face is really just a triangle with a base of 24, and a height of 16.


`\bf \left[(1)/(2)(\stackrel{b}{24})(\stackrel{h}{16}) \right]+\left[(1)/(2)(\stackrel{b}{24})(\stackrel{h}{16}) \right]+\left[(1)/(2)(\stackrel{b}{24})(\stackrel{h}{16}) \right]+\left[(1)/(2)(\stackrel{b}{24})(\stackrel{h}{16}) \right] \\\\\\ \textit{or just }\qquad 4\left[(1)/(2)(\stackrel{b}{24})(\stackrel{h}{16}) \right]\impliedby \textit{lateral area of the pyramid}`

Answer 2

Lateral surface area of pyramid is 768
`cm^2`

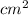
Explanation:

Given: Pyramid with Square base.

Side of square = 24 cm

Slant height = 16 cm

To find: Lateral surface area of pyramid

Figure of pyramid is attached.

Pyramid with square base has triangle in sides.

∴Lateral surface are of Pyramid = sum of area of all triangles

slant height of pyramid becomes height of triangle and side of square becomes base of triangle. Also all traingle are on equal side so, they have equal area.

Area of triangle =
`(1)/(2)*base*height`

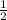
⇒ Lateral surface area of pyramid = 4 × area of triangle

Lateral surface area of triangle =
`4*(1)/(2)*base*height`

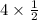
Base of triangle, AB = 24 cm and Height of triangle, OM = 16 cm

putting these value we get,

Lateral Area of Pyramid =
`4*(1)/(2)*24*16`

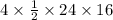
= 768
`cm^2`

Therefore, Lateral surface area of pyramid is 768
`cm^2`