Angle bisector theorem states that the ratio of the arms of the angle which is bisected is equal to the ratio of the sides intersected by the angle bisector
As CD is the bisector of <ACB
We shall use the angle bisector theorem to find the value of x.
According to the angle bisector theorem
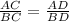
Substituting the values we get
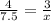
Cross multiplying we get
4x= 3 × 7.5
4x = 22.5
x = 22.5/4
x= 5.625
Hence the value of x shall be 5.625