We have to simplify the given expression:
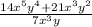
Dividing the terms of the numerator by the given term of denominator individually, we get
=
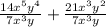
By using the laws of exponent,
 , we get
, we get
=
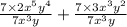
=

=

=
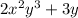
Therefore, the simplification of the given expression is
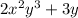 .
.
So, Option 3 is the correct answer.