Question

Explain step by step how to make a repeating decimal become into a fraction form?

Answer 1

Suppose we have the repeat decimal 0.123232323.... or 0.123 with a line over the repeated part (check the diagram)
- The first thing we need to do is identify the part of the decimal that repeats, 23 in our case.
- Second, we are going to assign a variable to our original decimal:
`x=0.123232323...`.
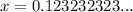
- Third, we are going to multiply both sides by a power of ten whose denominator will be the number of repeating digits. We know that we have 2 repeating digits (23), so we are going to multiply both sides by
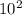
`10 ^(2)`, and
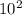
`10 ^(2)` is just 100; therefore we get:

`100x=(100)(0.123232323...)`

`100x=12.32323232...`
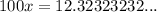
- fourth, subtract our original equation from the second step from the one from above:

`\left \{ {{100x=12.323232...} \atop {-x=1.123232} \right.`
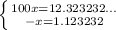
Now we can cancel the repeated decimals to get:

`\left \{ {{100x=12.3} \atop {-x=0.1}} \right.`

`99x=12.2`

`x= (12.2)/(99)`
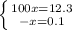
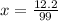
- Last but not least multiply both numerator and denominator by a power of ten equals to the decimal digits in the numerator:

`x= (12.2(10 ^(1)) )/(99(10 ^(1)) ) = (122)/(990)`

We now know how to convert a repeating decimal to a fraction.