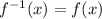Answer:
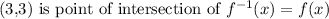
Explanation:
If f(x) and it's inverse function
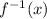 plot on same coordinate plane.
plot on same coordinate plane.
Both graph intersect at line y=x because y=x is line of symmetry of inverse function.
Intersection of
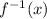 and f(x) would be x and y coordinate same.
and f(x) would be x and y coordinate same.
Therefore,
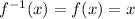
We are given four options. Let we check each one.
Option 1: (0,-2)
x=0 and y=-2 , 0≠-2
This is false.
Option 2: (1,-1)
x=1 and y=-1 , 1≠-1
This is false.
Option 3: (2,0)
x=2 and y=0 , 2≠0
This is false.
Option 4: (3,3)
x=3 and y=3 , 3=3
This is true.
Thus, (3,3) is point of intersection of