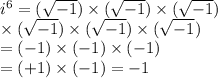Question

Please explain how to do this?
i^6=
A. -1
B. 1
C. -i
D. i

Answer 1

Ok, so "i" was invented to allow algebra math problems to continue, despite containing the square root of a negative. The square root of a negative can't be solved because anything squared will become positive.
In other words, square root of -25 is not solvable because -x * -x = +x^2
To make solving manageable, mathematicians created the square root of negative one (-1) as this imaginary entity (i).
Let's use that square root of -25 again:

`√( - 25) = √(25) \: * √( - 1) \\ √(25) \: * i = 5i`

So in plain terms, it's as simple as this:

`i = √( - 1) \\ {i}^(2) = √( - 1) * √( - 1) = - 1 \\ {i}^(3) = √( - 1) * √( - 1) * √( - 1) \\ {i}^(3) = - 1\: * √( - 1) = - √( - 1) = - i`
without doing too many examples, I want you to understand this pattern:
whenever the exponent of i is EVEN, then the answer will not have a radical !!
Why? because every couplet of i's will = i^2 which = -1
BUT an ODD numbered exponent of i will always leave that extra i after all the couplets become -1.

`{i}^(even \: ) = - 1 \: or \: 1 \: (depends) \\ {i}^(odd) = - i \: or \: i = \: alternates \\ between \: + and \: - \: i`
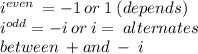
It's a little complicated in that every couplet will become -1, but if you have pairs (2) of COUPLETS, then -1×-1 = 1
So a couplet (2) × a pair (2) of couplets = 2×2=4
That means that if the even exponent is divisible by 4 (4, 8, 12, 16, etc.), then the answer will ALWAYS be +1. Otherwise the even exponent 2, 6, 10, 14, etc.) will result in a -1.

Now for our actual problem!!

`{i}^(6) \: and \: 6 \: is \: even \:and \: not \: divisible \\ by \: 4 \: therefore \: our \: rule \: is \\ {i}^(6) = - 1`
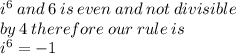
Proof:

`{i}^(6) = ( √( - 1) ) * ( √( - 1) ) * ( √( - 1) ) \\ * ( √( - 1) ) * ( √( - 1) ) * ( √( - 1) ) \\ = ( - 1) * ( - 1) * ( - 1) \\ = ( + 1) * ( - 1) = - 1`