The first statement is true. Reasoning below.
= = =
We want to find the area of a fixed circle, so we can throw out the last option. If

changes at all, then so does the area of the circle.
For

to increase would require using a circumscribed polygon with less sides. Again, the circle is fixed, so only a certain length

can fit inside the circle. This eliminates the third option.
Note that if we use a regular hexagon, then

automatically, because the component triangles that make up the hexagon are equilateral. Increasing

would require that we use a polygon with more sides, which would simultaneously make

stray away from

. In other words, if

increases, then

decreases, so we can never eventually have

(

is fixed).
That leaves the first option. Indeed, as

increases, we get a polygon that looks increasingly rounder and more like a perfect circle. At the same time, that means

gets larger, but would be bounded above by the circle's perimeter. So as

increases indefinitely, it will eventually "be equal" (in the limit sense) to

, so that
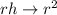
.