Question

Suppose the line of best fit is being found for some data points that have an r-value of 0.793. If the standard deviation of the x-coordinates is 5.591, and the standard deviation of the y-coordinates is 2.772, what is the slope of the line to three decimal places?

Answer 1

0.393

Step-by-step explanation:

Answer 2

Answer: 0.393

Step-by-step explanation: If the given quantities are r-value (or Pearson's coefficient) and the standard deviations of x and y coordinates, we'll use the following formula for slope:


`m = (rs_y)/(s_x)`

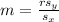
where:
m = slope of the best fit line
r = r-value = 0.793

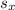
`s_x` = standard deviation of x-coordinates = 5.591

`s_y` = standard deviation of y-coordinates = 2.772

So, the slope is calculated as follows:


`m = (rs_y)/(s_x) \\ = ((0.793)(2.772))/(5.591) \\ \boxed{m \approx 0.393}`

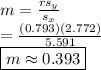
Hence, the slope in 3 decimal places is 0.393.