Question

Yolanda conducted a poll and out of the 270 people she surveyed, 60% were planning to live in their town for the rest of their lives. She decided to conduct another poll asking the same question, and again found that 60% of the people in the second poll were planning to live in their town for the rest of their lives. If both polls had a confidence level of 90% (z*-score of 1.645), and the margin of error was 3 times greater in the second poll, approximately how many people were surveyed in the second poll? E = z* and n = (1 – ) •

Answer 1

The formula for margin of error is:

`E=z \sqrt{ (p*q)/(n) }`

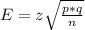
From this equation, we can eliminate n, which will be:

`n= (p*q)/( ( (E)/(z) )^(2) )`

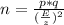
We have to find the number of subjects (n) for the second poll.
We have p = 0.6
q = 1 - p = 0.4
z = 1.645
E for second poll is unknown.

It is given that Margin of error of second poll is 3 times the margin of error of first poll. So if we find margin of error of first poll, we can use it to calculate margin of error of second poll.

Using the data for first poll to calculate E:

`E=1.645 \sqrt{ (0.6*0.4)/(270) }=0.049`

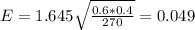
Margin of error for second poll will be = 3 x 0.049 = 0.147

Now using this value to calculate number of subjects in second poll:


`n= (0.6*0.4)/( ( (0.147)/(1.645) )^(2) ) = 30`

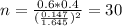
Thus approximately 30 subjects were surveyed in the second poll.

Answer 2

The sample size can be calculated by the following formula:


`s= (z(p)(1-p))/( E^(2) )` where s is the sample size, z is the z-score of the confidence level, p is the decimal form of the percentage who picked a certain choice in the poll, and E is the margin of error expressed as a decimal.

We first find the margin of error in the original sample size of 270.


`270= (1.645(0.60)(0.40))/( E^(2))`

`E^(2)= (1.645(0.60)(0.40))/(270)=0.00146`

`E=0.038`

Since the new sample had 3 times the margin of error of the first poll, we will use 3(0.038) or 0.114 as the margin of error of the new sample. We then compute for the sample size using the same formula.


`s= (1.645(0.60)(0.40))/( 0.114^(2) )=30`

ANSWER: 30 people were surveyed on the second poll.