Explanation:
1. the perfect squares in this case are
a²+26a+169 = (a+13)²
a²+14a+49 = (a+7)²
First and fourth option are correct.
2. factorise 4p²+36p+81
Product = 324 and sum = 36
numbers are 18 and 18
∴ 4p²+18p+18p+81
⇒ 2p(2p+9) +9(2p+9)
⇒ (2p+9)(2p+9) ⇒
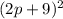
3. Factor
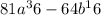
As
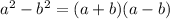
∴
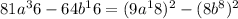
=
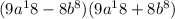 (Option B)
(Option B)
4. The differences between two squares is such that;
a²-b² = (a+b)(a-b)
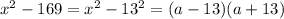 , and
, and
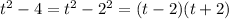
First and third option correct.