Answer : The maturity value of a loan is, $7103.73
Step-by-step explanation :
Given:
Principle = $6787
Rate = 14 % per year
Time = 4 months =
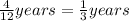
First we have to determine the simple interest.
Formula used :
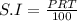
where,
P = principle
R = interest rate
T = time
S.I = simple interest
Now put all the given values in the above formula, we get:
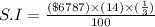
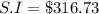
Now we have to calculate the maturity value of a loan.
Maturity value of a loan = Principle + Simple interest
Maturity value of a loan = $6787 + $316.73
Maturity value of a loan = $7103.73
Thus, the maturity value of a loan is, $7103.73